img
img
Comments...

img Frequency Response (Nyquist Diagrams)

The figure below shows the Nyquist plot for a transfer function. The poles (x) and zeros (o) of the transfer function are plotted on the complex plane. In addition the transfer function is multiplied by an adjustable gain (in green).

Use the controls to change the order of the numerator (number of zeros) and denominator (number of poles). Drag the poles and zeros on the complex plane to change their location. Complex poles or zeros are shown in the transfer function using the standard form s2 + 2ζ ωns + ωn2

G(s) = 1.00
1____________ s3 + 10 s2+ 12s + 24
poles: 2   zeros: 1

Questions:

  1. Using Nquist determine if a system with poles at -3 and -9 will be stable. (answer)
    The nyquist plot is:
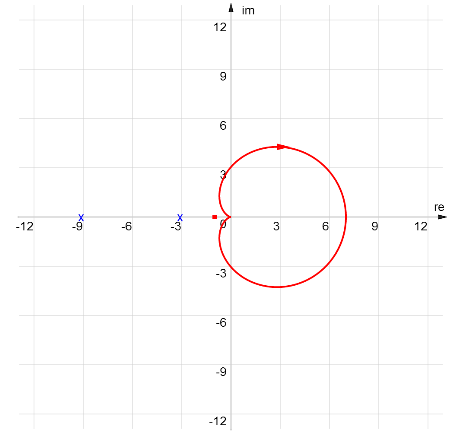      img which has no encirclements of the -1 point. In additions the open-loop system has no unstable poles. Therefore:
    N = CL - OL → 0 = CL - 0 → CL = 0;
    Thus the closed-loop system is stable. This matches what we know from the root locus for the system.
  2. Using Nquist determine if a system with poles at -3 and 6 will be stable. (answer)
    The nyquist plot is:
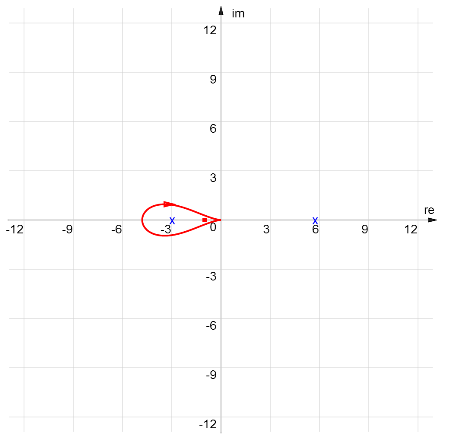      img which has one encirclement of the -1 point. In additions the open-loop system has one unstable pole. Therefore:
    N = CL - OL → 1 = CL - 1 → CL = 2;
    Thus the closed-loop system has two unstable poles. This matches what we know from the root locus for the system.
  3. Using Nquist determine if a system with poles at -3 and 1.5 will be stable. (answer)
    The nyquist plot is:
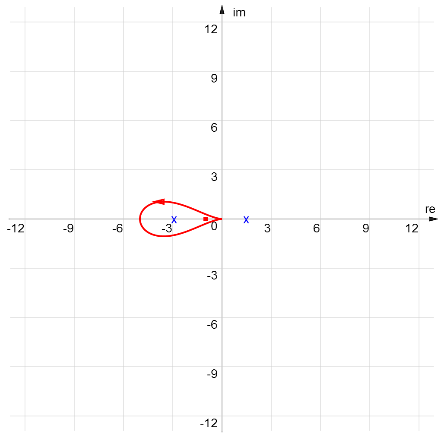      img which has one encirclements of the -1 point in the counter-clockwise direction. In additions the open-loop system has no unstable poles. Therefore:
    N = CL - OL → -1 = CL - 1 → CL = 0;
    Thus the closed-loop system has no unstable poles. This matches what we know from the root locus for the system.