Comments...

PID Controller

A  linear positioning system is commonly used in manufacturing equipment such as a CNC mill . These system often use a drive motor and linear screw to move the cutter across the material. The position of the cutter is often controlled using a PID controller. The controller measures the position of the cutter, compares it to the desired cutter position and adjust the input to the drive motor accordingly. A simplified block diagram of such a system is shown in Fig 3.1.2.

Figure 3.1.2 Block Diagram of Positioning System

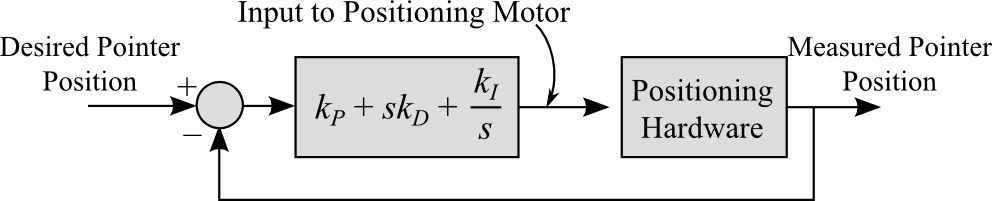
A simulation of a CNC system is shown below. As you move the slider on the bottom of the system (the desired position), the controller attempts to moves the cutter (measured position) to match the position of the slider. Experiment with the slider and PID gains. Notice the response of the cutter as it tracks the slider. Also notice how different PID gain values affect the system response.

Questions:

1. In a proportional controller k_D = k_I = 0. How does the value of k_P affect the systems response. (answer).
   k_P tends to affect the speed of the system. In this system increasing k_P decreases the settling time of the system. However, increasing k_P also decreasing the system's damping which results in more overshoot.

   Notice that increasing k_P also decreases the steady-state error of the system. This is typical. As you increase the system gain you decrease the error. In general, however, simply increasing k_P is not enough to completely eliminate steady-state error. You must add in integral control.

2. In a PD controller k_I = 0. How does the value of k_D affect the systems response. Experiment by setting k_{P = 5} and changing k_D. (answer)

   k_D tends to affect the damping of the system. Set k_P = 5 and k_D=0. Note how long it take for the system to come to rest (T_settling ≈ 2 seconds).

   Now set k_D = 0.5. Notice how the system damping changes but the settling time remains the same. However, as you continue to increase k_D the systems damping increases eventually lengthening the settling time.

   
   

   One problem with k_D is that it tends to amplify system noise. This should make sense. Noise tends to occur at high frequencies. The derivative of a fast changing (high frequency) value is a large number. In this system you can see the detrimental affects of k_D once we add in k_I

3. In a PI controller k_D = 0. How does the value of k_I affect the systems response. (answer).

   k_I can be used to reduce tracking error and for a step input it can it can complete eliminate the steady-state error. Set k_P = 5 and observe the steady-state error (the difference between the pointer location and the slider). Then set k_I=5. Notice the steady state error.

   The disadvantage of using k_I is that small values tend to slows down the response and large values can destabilize the system. Try increasing k_I and observe how the response changes

4. A full PID controller is sometimes necessary to get the desired response. Experiment with different PID values until you can get a system that has no steady-state error to a step input and no overshoot. Be careful since certain values of either k_D or k_I can destabilize the system. (answer).

   Try the values:

   k_P=15
   k_D=1
   k_I=60

   Notice how changing k_P in PID controller has a slightly different affect then changing k_P in a strictly proportional controller. The addition of k_I increases the overall order of the underlying differential equation and so the system response to a given parameter.